How to Predict Sales Using the ARIMAX Algorithm


For most businesses, decision-making is closely tied to forecasting outcomes, which are essential for activities like production planning and inventory optimization.
To achieve this, time series analysis is commonly employed. Its mathematical models determine how future values depend on past values within the same process. Then, the analysts construct forecasts based on the identified dependencies.
Time series analysis is most effective for short-term forecasting. As the forecast horizon extends, models begin to predict new values based on their previous predictions. While this is acceptable over shorter periods, forecast accuracy diminishes significantly with longer horizons due to accumulating errors.
It's also crucial to consider limitations. Time series analysis methods are best suited for stochastic (stationary) processes where the probability distribution remains consistent over time. For instance, we can use them to forecast sales volumes.
There are specific models within this category:
- ARIMA: An autoregressive integrated moving average model.
- ARIMAX: This model additionally considers the impact of exogenous (eXogenous) factors affecting the change in the initial indicator.
The abbreviations ARIMA/ARIMAX stand for:
- AR — Autoregressive: This part indicates that the predicted values of the variable are based on its previous values.
- I — Integrated: Indicates that the model studies not the values of the process, but the changes in its indicators relative to each other, often by differencing to achieve stationarity.
- MA — Moving Average: This is a filter that smooths the outliers of the time series by replacing each value with the arithmetic mean of several neighboring values.
- X — EXogenous: Indicates including external factors that influence the forecast.
Considering external factors is crucial for high-accuracy forecasting. However, collecting and processing this data often takes time, and in some cases, predicting their behavior is challenging.
For example, when analyzing the sales of winter sports goods, air temperature is an important parameter, but everyone knows that meteorologists are regularly wrong with their forecasts even for the day ahead. When planning for months, weather data's accuracy is too low to consider.
In this article, we'll explore an example of forecasting using the ARIMA model in Megaladata. Here, only the historical data of the indicator we're forecasting is needed; no additional data is required.
Let's leave preprocessing and further use of data aside for now and understand how the ARIMAX component works.
Input Data
To obtain a correct forecast, a sufficient amount of data on previous sales is required. Using outdated information affects the forecast reliability. Additionally, you need more data as the length of the forecast interval increases. In our case, a forecast for five months ahead requires information on at least several annual periods from the past.
Here is the table with the source data. It has the following columns:
- Date: The first day of each month, since the time interval chosen is a month.
- Sales (USD): Total sales of winter sports goods for the month.
| Date | Sales (USD) |
|---|---|
| 01.05.15 | 2501.28 |
| 01.06.15 | 2251.28 |
| 01.07.15 | 1842.66 |
| 01.08.15 | 2007.93 |
| 01.09.15 | 2652.75 |
| 01.10.15 | 3392.86 |
| 01.11.15 | 3906.78 |
| 01.12.15 | 4179.45 |
Model Building
Megaladata has a special ARIMAX component that includes an ARIMA mathematical model with exogenous inputs that will be included in the analysis. If no external data is input, it effectively turns into ARIMA.
Let's add this component to the workflow and feed the node input with initial data.
Now we need to configure the ARIMAX component, to receive forecast data. The first window in the configuration wizard is 'Configure Input Columns'. Here, each source data column gets one of three possible values:
- Unspecified: Automatically set for all fields by default. In our case, we'll keep this value only for the 'Date' field.
- Input: Needs to be set for fields that correspond to an external factor; in our example, there are none.
- Forecast: This can be set only for one field, in our case, 'Sales'.

After setting the input columns, normalization of input and output fields is available. However, in most cases neither time field data nor external parameters require it.
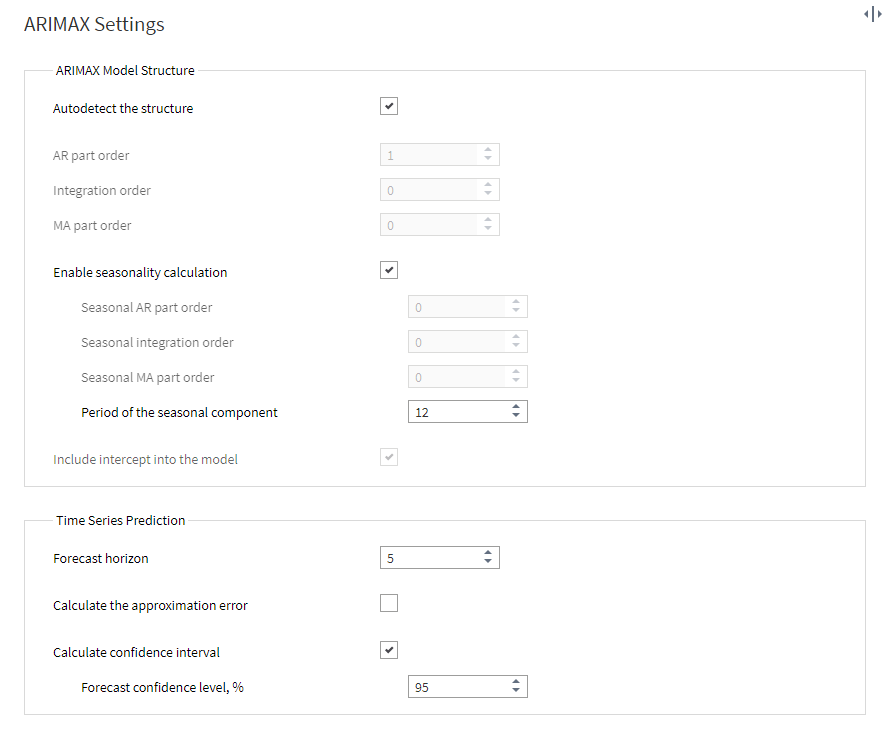
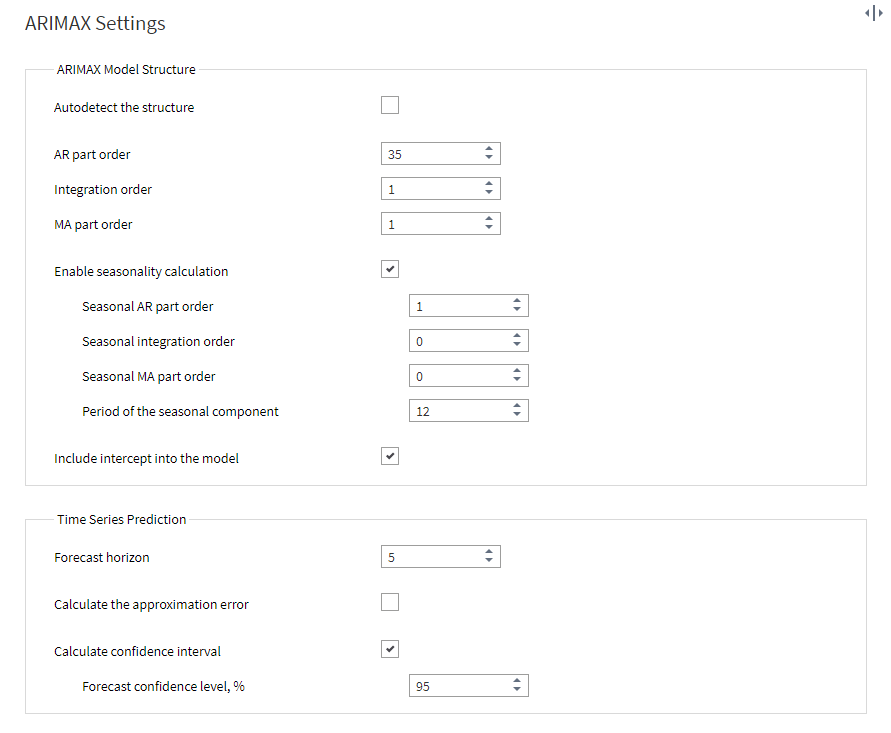
The main configuration can be performed in the ‘ARIMAX Settings’ window. If some forecast criteria are missing, you can tick the box ‘Autodetect the structure’, and the component will calculate the necessary parameters for your data.
By default, the forecast horizon is set to 1, meaning we get a forecast for one period ahead. To get a better understanding of the node's operation, let's change this value to 5.
We do not run the node immediately after saving its settings. First, we need to train it.
This can be done through the command ‘Retrain node’ in the context menu.
Prediction Results
The ARIMAX node has three output ports:
- Model output
- Model coefficients
- Summary
After running (or training) the node, you can open 'Quick View' on the first output port and see that the original data has been supplemented with the following output columns:
- Sales | Prediction: Forecast of sales based on previous periods.
- Sales | Lower bound: Lower boundary of sales forecast based on previous periods.
- Sales | Upper bound: Upper boundary of sales forecast based on previous periods.
- Sales | Approximation error: The average deviation of the calculated values from the actual values. This field will be displayed if the 'Calculate the approximation error' box is ticked.
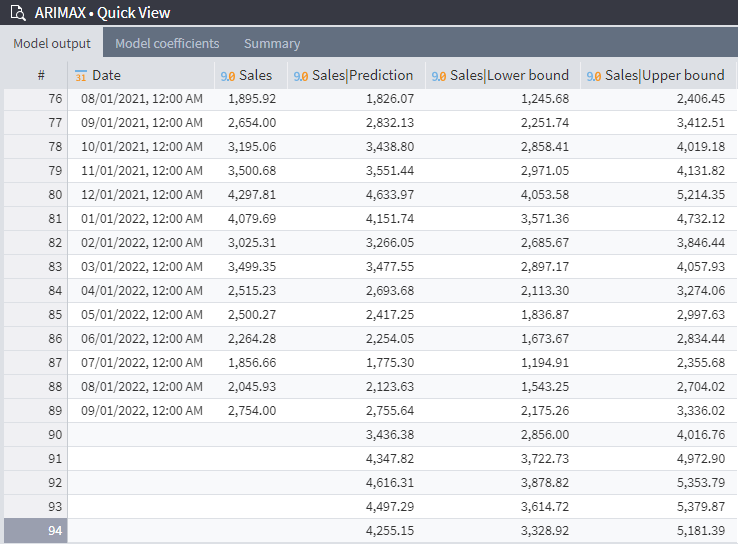
The forecast data will be calculated for both months with known sales volumes and new periods. Note that at the very beginning of the table, the new (forecast) columns will have empty cells; their number depends on the value set in the 'AR part order' field (this can be found in ARIMAX settings).
The second output port contains a table with the model coefficients, and the third one — a summary of variable values: the number of samples, errors on the training set, information criteria, coefficients of determination, and degrees of freedom.
The three output ports provide comprehensive information about the performed prediction, but the tabular representation can be difficult to perceive, so visualizers can be helpful.
However, before plotting, it is necessary to fill in the time series values for the new rows. Otherwise, the forecast graph will be displayed only on the original time period, and the values on the forecast horizon will not be included. To do this, let's add the Calculator component.
In the Calculator settings (Edit Expressions), create a variable, AllDates, which will contain all the values of the time series. We will perform the calculation using the IF function: If the date field is empty, the AddMonth function will add the required number of months to the last known value; otherwise, it will use the date specified in the field.
To calculate the number of months, first determine the difference between the current row number (using the RowNum() function) and the count of unique values in the Date field (using the Stat("Date", "UniqueCount") function). Then, add 2 to this result: row numbering begins at 0, and the count of unique values also includes an empty value for rows added after the forecast.
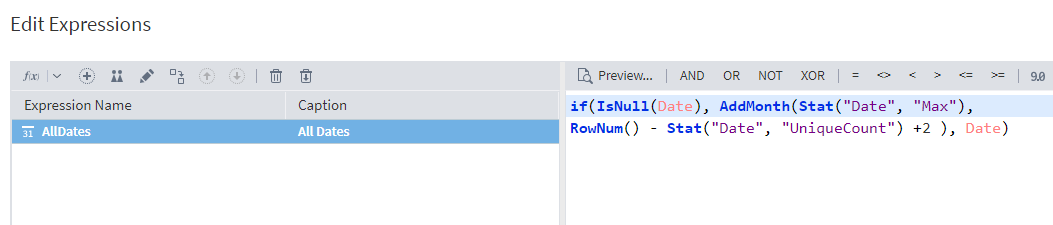
When we execute the Calculator component, it will output the table with a new 'All Dates' column added.
Graph Construction
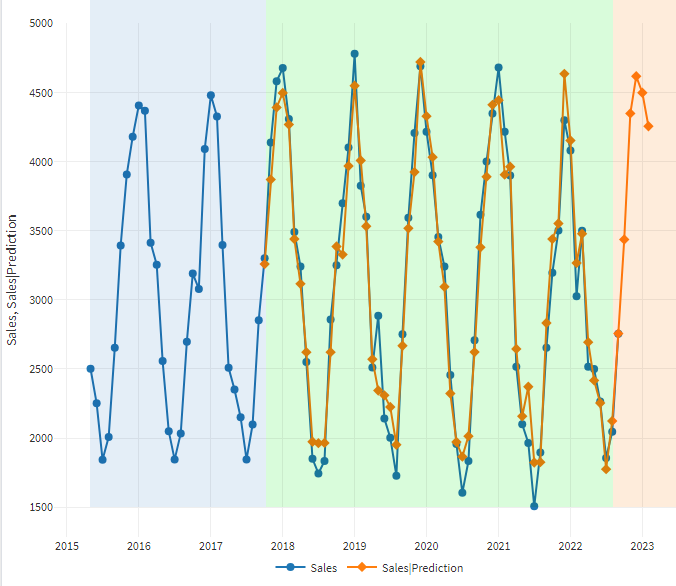
To see the forecast values and their correlation with the actual indicators, let's plot the initial values of sales volume and the forecast of this value calculated using the ARIMAX component.
The graph will show the curves of forecast and initial sales volumes in dollars.
Analysing the Results
The graph is plotted for three different time periods. (We have highlighted them with colors for your convenience.)
- Model training: In this period (blue), we can only plot the actual data curve.
- Forecast and actual values: The graph on the green background simultaneously displays two curves, allowing you to visually assess how close the forecast values, generated by ARIMAX, are to the actual values.
- Forecast horizon: The forecast curve is displayed on amber background.
The training stage set in the ARIMAX node was 29 months (about 2 years). At the second stage, we can see that the graphs of sales volume and its forecast have the same shape, but the values at some points are significantly different. The forecast curve at the third stage visually repeats the shape of the curve of initial sales values.
Increasing Forecast Accuracy
If the accuracy of the forecast using the automatically set parameters is not satisfactory, you can manually adjust these values.
It's crucial to understand that there are no universal rules applicable to all forecasting tasks; each dataset might require different settings. The documentation offers a comprehensive explanation of the ARIMAX structure along with definitions for each customizable parameter.
Let's adjust the parameters in the ARIMAX configuration window as illustrated in the figure below.
Next, we will need to retrain this node.
Once we retrain the node, the forecast values will be recalculated. In the visualizer, you'll notice that the curve graphs for the two time periods have become nearly identical. This visual similarity suggests an increase in forecast accuracy.
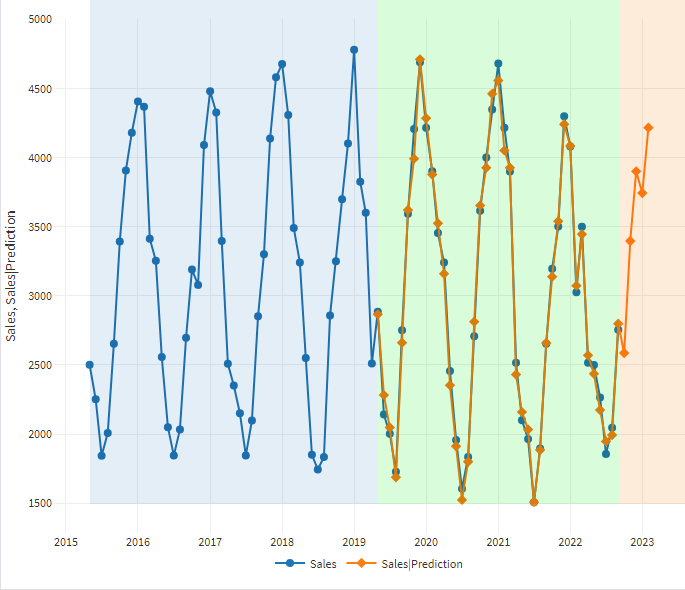
To confirm that the forecast has improved in accuracy, let's open the "Summary" tab (Quick View of the third output port of the ARIMAX node). You'll see that the mean absolute percentage error (MAPE, or Mean Relative Error, MRE, as used in Megaladata) in the training set has significantly decreased compared to previous values.
MAPE compared
Automating Forecasting in Megaladata
In this example, we created a forecast for the sales volume of seasonal winter sports products using the ARIMA model.
Using the automatically set parameters of the ARIMAX component, we achieved an accurate forecast with minimal input data. Furthermore, we enhanced the forecast's accuracy by manually adjusting the parameters.
The ARIMAX component is notable for its ease of use and speed. Simply input your data, optionally include forecasting indicators, and within seconds, you'll have an accurate forecast. Additionally, Megaladata allows you to plot charts of both actual and forecasted values, enabling a visual assessment of the results.
See also



